Cube-square identities
> restart;
Odd squares first
> # see ?polynomial for Maple's use of 'quo' and 'rem' with polynomials
> expand(((27*x^2 + 27*x + 7 - 1)/3)^3);
Now, this was a bit odd, to say the least:
>
quo(729*x^6+2187*x^5+2673*x^4+1701*x^3+594*x^2+108*x+8,
27*x^2+27*x+7, x, 'R0');
> R0;
> floor(31/27);
I had to resort to this to get the odd square identity :
>
(729*x^6+2187*x^5+2673*x^4+1701*x^3+594*x^2+108*x+8)
- expand((27*x^2+27*x+7)*(27*x^4+54*x^3+38*x^2+11*x+1));
> factor(4*x^2+4*x+1);
A look at the quotient quartic:
> factor(27*x^4+54*x^3+38*x^2+11*x+1);
Thus one has the following identity :
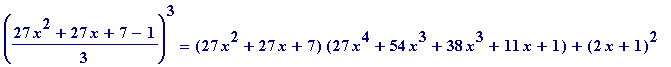
Now the even squares ( seven cases)
(0) The zero-th of the seven even-square producing quadratics:
> expand(((108*x^2 + 1 - 1)/3)^3);
> quo(46656*x^6, 108*x^2+1, x, 'r0');
> r0;
I had to resort to this to get the zero-th of the even square identities :
> (46656*x^6) - expand((108*x^2+1)*(432*x^4-4*x^2));
That, of course, is identically
.
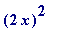Thus one has the following identity :
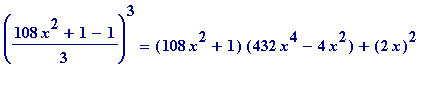
(1) The i = 1 case of the seven even-square producing quadratics:
> expand(((756*x^2+648*x+139 - 1)/3)^3);
>
quo(16003008*x^6+41150592*x^5+44035488*x^4+25100928*x^3+8038224*x^2
+1371168*x+97336, 756*x^2+648*x+139, x, 'r1');
>
16003008*x^6+41150592*x^5+44035488*x^4+25100928*x^3
+8038224*x^2+1371168*x+97336 - expand((756*x^2+648*x+139)*
(21168*x^4+36288*x^3+23252*x^2+6600*x+700));
where the constant term '700' is obtained from the 'r1' quotient constant term:
> floor(18907/27);
> factor(196*x^2+168*x+36);
is, in fact,
.
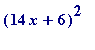Thus one has the following
identity
:
=
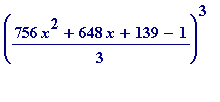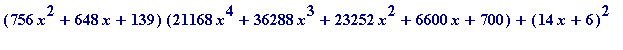
A look at the quotient quartic:
> factor(21168*x^4+36288*x^3+23252*x^2+6600*x+700);
That quadratic has discriminant:
> 162^2 - 4*189*35;
is
.
Interesting...
(2) The i = 2 case of the seven even-square producing quadratics:
> expand(((756*x^2+864*x+247 - 1)/3)^3);
>
quo(16003008*x^6+54867456*x^5+78327648*x^4+59595264*x^3+25487568*x^2+
5809536*x+551368, 756*x^2+864*x+247, x, 'r2');
>
16003008*x^6+54867456*x^5+78327648*x^4+59595264*x^3+25487568*x^2+
5809536*x+551368 - expand((756*x^2+864*x+247)*
(21168*x^4+48384*x^3+41396*x^2+15712*x+2232));
where the constant term '2232' is obtained from the 'r2' quotient constant term:
> floor(60271/27);
> factor(196*x^2+224*x+64);
is, in fact,
...
.
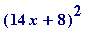Thus one has the following
identity
:
=
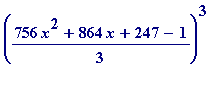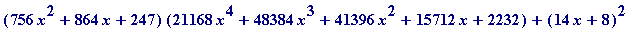
A look at the quotient quartic:
> factor(21168*x^4+48384*x^3+41396*x^2+15712*x+2232);
That quadratic has discriminant:
> 216^2 - 4*189*62;
is also
...
(3) The i = 3 case of the seven even-square producing quadratics:
> expand(((1404*x^2+864*x+133 - 1)/3)^3);
>
quo(102503232*x^6+189236736*x^5+145364544*x^4+59470848*x^3+13666752*x^2
+1672704*x+85184, 1404*x^2+864*x+133, x, 'r3');
>
102503232*x^6+189236736*x^5+145364544*x^4+59470848*x^3+13666752*x^2
+1672704*x+85184 - expand((1404*x^2+864*x+133)*
(73008*x^4+89856*x^3+41324*x^2+8416*x+640));
where the constant term '640' is obtained from the 'r3' quotient constant term
> floor(17293/27);
> factor(676*x^2+416*x+64);
is, in fact,
...
.
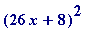Thus one has the following
identity
:
=
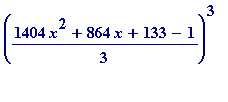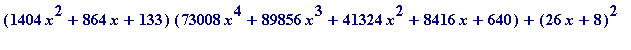
A look at the quotient quartic:
> factor(73008*x^4+89856*x^3+41324*x^2+8416*x+640);
Ah! Interesting! Two quadratics. That's novel...
The first dfiscriminant:
> 216^2 - 4*351*32;
Oh! That's
...
And the other one:
> 32^2 - 4*52*5;
Oh! That's
...
(4) The i = 4 case of the seven even-square producing quadratics:
> expand(((1404*x^2+1944*x+673 - 1)/3)^3);
>
quo(102503232*x^6+425782656*x^5+736729344*x^4+679684608*x^3+352622592*x^2
+97542144*x+11239424, 1404*x^2+1944*x+673, x, 'r4');
>
102503232*x^6+425782656*x^5+736729344*x^4+679684608*x^3+352622592*x^2
+97542144*x+11239424 - expand((1404*x^2+1944*x+673)*
(73008*x^4+202176*x^3+209804*x^2+96696*x+16700));
where the constant term '2232' is obtained from the 'r4' quotient constant term:
> floor(450913/27);
> factor(676*x^2+936*x+324);
is, in fact,
...
.
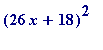Thus one has the following
identity
:
=
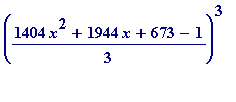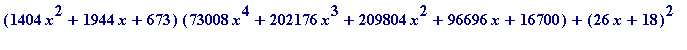
A look at the quotient quartic:
> factor(73008*x^4+202176*x^3+209804*x^2+96696*x+16700);
Again, two more quadratics...
The first discriminant:
> 486^2 - 4*351*167;
is again
,
while the other one is:
> 72^2 - 4*52*25;
is once again
...
(5) The i = 5 case of the seven even-square producing quadratics:
> expand(((2052*x^2+864*x+91 - 1)/3)^3);
>
quo(320013504*x^6+404227584*x^5+212308128*x^4+59346432*x^3+9311760*x^2
+777600*x+27000, 2052*x^2+864*x+91, x, 'r5');
>
320013504*x^6+404227584*x^5+212308128*x^4+59346432*x^3+9311760*x^2
+777600*x+27000 - expand((2052*x^2+864*x+91)*
(155952*x^4+131328*x^3+41252*x^2+5728*x+296));
where the constant term '2232' is obtained from the 'r4' quotient constant term:
> floor(8011/27);
> factor(1444*x^2+608*x+64);
is, in fact,
...
.
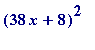Thus one has the following
identity
:
=
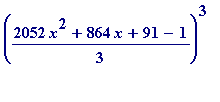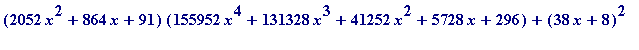
A look at the quotient quartic:
> factor(155952*x^4+131328*x^3+41252*x^2+5728*x+296);
Ah! It's irreducible...
(6) The i = 6 case of the seven even-square producing quadratics:
> expand(((2052*x^2+3240*x+1279 - 1)/3)^3);
>
quo(320013504*x^6+1515853440*x^5+2991372768*x^4+3147880320*x^3
+1863047952*x^2+587982240*x+77308776, 2052*x^2+3240*x+1279, x, 'r6');
>
320013504*x^6+1515853440*x^5+2991372768*x^4+3147880320*x^3
+1863047952*x^2+587982240*x+77308776 - expand((2052*x^2+3240*x+1279)*
(155952*x^4+492480*x^3+582980*x^2+306600*x+60444));
where the constant term '2232' is obtained from the 'r4' quotient constant term:
> floor(1632007/27);
> factor(1444*x^2+2280*x+900);
is, in fact,
...
.
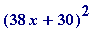Thus one has the following
identity
:
=
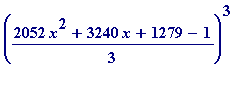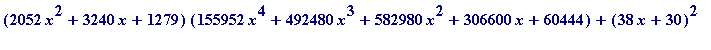
A look at the quotient quartic:
> factor(155952*x^4+492480*x^3+582980*x^2+306600*x+60444);
Again, also irreducible...
The values of the even squares
> restart;
> poly0 := R -> 108*R^2 + 1; # r = 2*R in 1+27*r^2
(1) Here r is defined by r = 2W = 14R + 6 or 8
>
i := 1:
poly||i := R -> expand((1+27*(14*R+6)^2)/7): # r=14*R+6
sort(poly||i(R));
>
i := 2:
poly||i := R -> expand((1+27*(14*R+8)^2)/7): # r=14*R+8
sort(poly||i(R));
>
(2) Here r is defined by r = 2W = 26R + 8 or 18
>
i := 3: poly||i := R -> expand((1+27*(26*R+8)^2)/13): # r=26*R+8
sort(poly||i(R));
>
i := 4: poly||i := R -> expand((1+27*(26*R+18)^2)/13): # r=26*R+18
sort(poly||i(R));
(3) Here r is defined by r = 2W = 38R + 8 or 30
>
i := 5: poly||i := R -> expand((1+27*(38*R+8)^2)/19): # r=38*R+8
sort(poly||i(R));
>
i := 6: poly||i := R -> expand((1+27*(38*R+30)^2)/19): # r = 38*R+30
sort(poly||i(R));
>
> for i from 0 to 6 do [i, poly||i(R)] od;
![[0, 108*R^2+1]](images/reduced TCD talk 9th Feb 2005603.gif){kind=small}
![[1, 756*R^2+648*R+139]](images/reduced TCD talk 9th Feb 2005604.gif){kind=small}
![[2, 756*R^2+864*R+247]](images/reduced TCD talk 9th Feb 2005605.gif){kind=small}
![[3, 1404*R^2+864*R+133]](images/reduced TCD talk 9th Feb 2005606.gif){kind=small}
![[4, 1404*R^2+1944*R+673]](images/reduced TCD talk 9th Feb 2005607.gif){kind=small}
![[5, 2052*R^2+864*R+91]](images/reduced TCD talk 9th Feb 2005608.gif){kind=small}
![[6, 2052*R^2+3240*R+1279]](images/reduced TCD talk 9th Feb 2005609.gif){kind=small}
>
i := 0: poly||i(x);
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 1: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 2: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 3: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 4: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 5: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>
i := 6: sort(poly||i(x));
for R from 0 to 10 do sqrt(((poly||i(R)-1)/3)^3 mod poly||i(R)) od;
>